Sine meaning – Sine, a pivotal trigonometric function, holds immense significance in the realm of mathematics and its practical applications. It serves as a fundamental building block for comprehending the behavior of waves, oscillations, and countless other phenomena in the world around us.
From its mathematical definition to its graphical representation, the sine function unveils a fascinating journey of discovery, exploration, and real-world relevance.
Sine Function: A Comprehensive Overview
The sine function is a fundamental trigonometric function that plays a crucial role in various fields, including engineering, physics, and music. It describes the vertical coordinate of a point on a unit circle as an angle is measured from the positive x-axis.
Definition
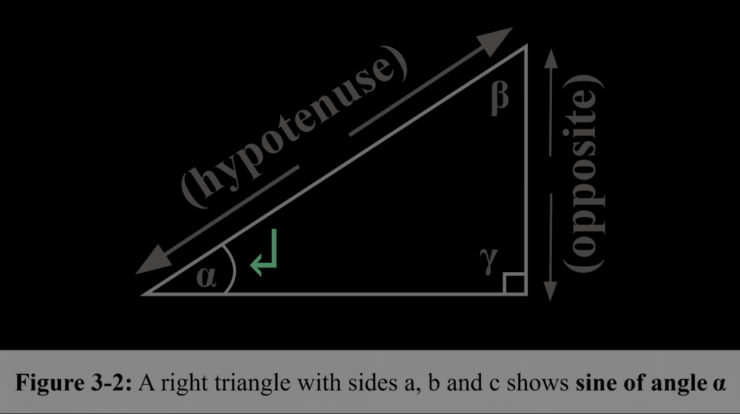
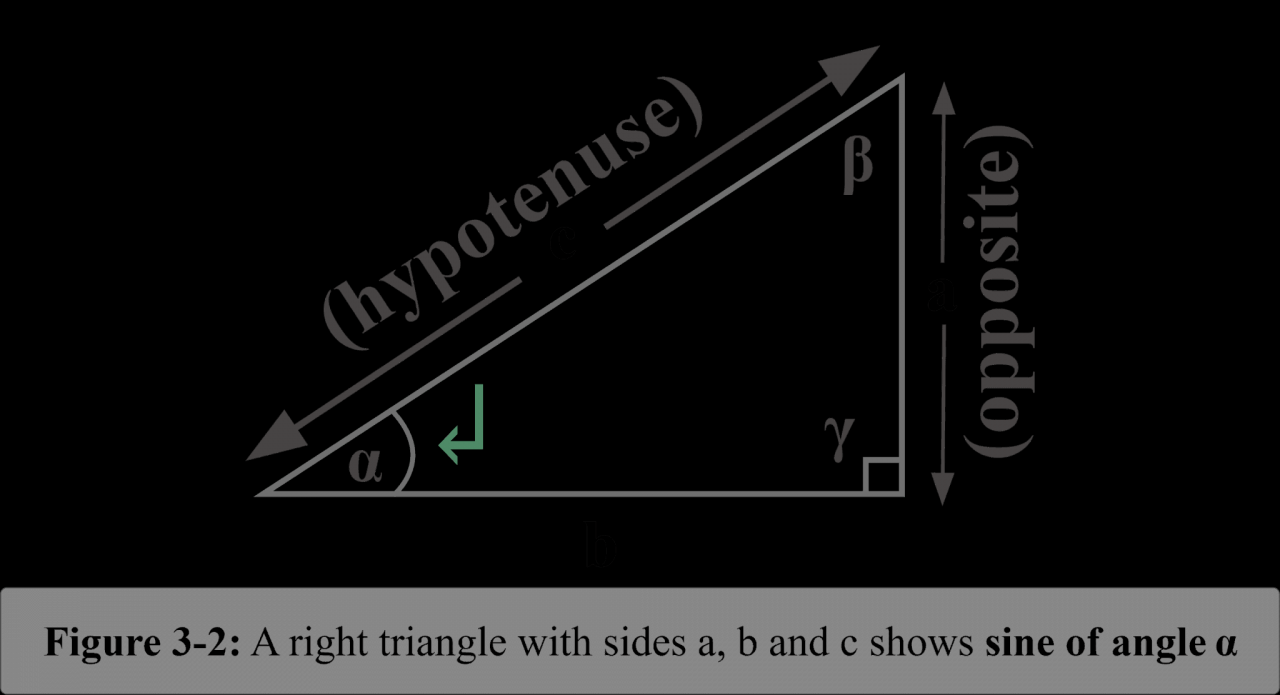
Mathematically, the sine of an angle θ is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle with that angle. In simpler terms, it represents the vertical displacement of a point moving around a unit circle as the angle increases.
Properties, Sine meaning
- The sine function is periodic with a period of 2π.
- It is an odd function, meaning that sin(-θ) = -sin(θ).
- The range of the sine function is [-1, 1].
| Function | Range | Period | Odd/Even |
|---|---|---|---|
| Sine | [-1, 1] | 2π | Odd |
| Cosine | [-1, 1] | 2π | Even |
| Tangent | (-∞, ∞) | π | Odd |
Graph
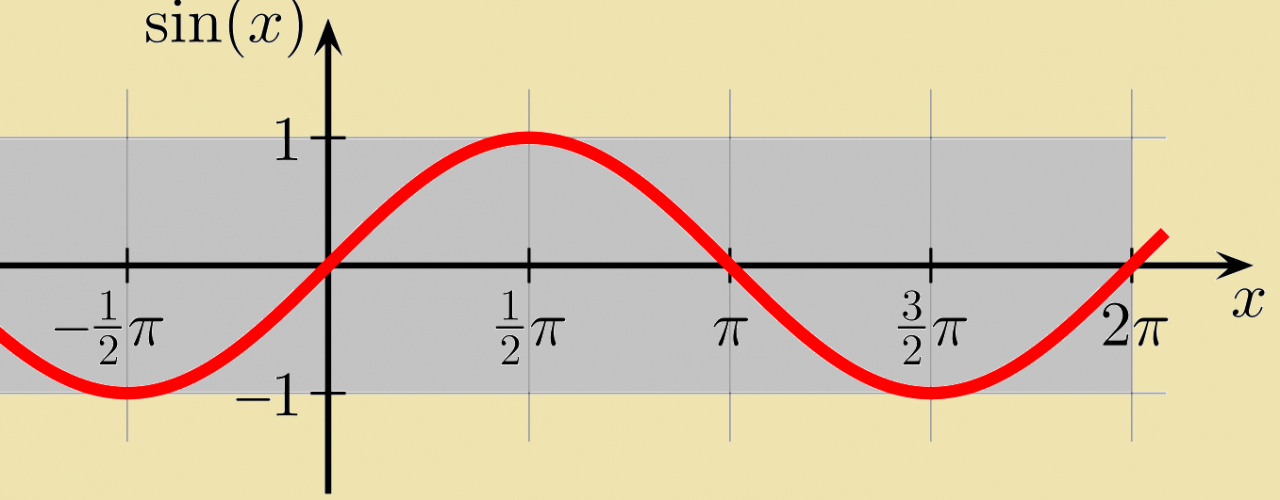
The graph of the sine function is a wave-like curve that oscillates between -1 and 1. It has a maximum value of 1 at θ = π/2 and a minimum value of -1 at θ = 3π/2.
Applications
The sine function has numerous applications in real-world scenarios:
- In engineering, it is used to analyze vibrations, sound waves, and electrical circuits.
- In music, it is used to describe the pitch of sound waves and create harmonic melodies.
- In physics, it is used to model the motion of objects in circular or oscillatory motion.
History
The sine function has a rich history, with its roots in ancient Greece. Hipparchus of Nicaea developed a table of chords in the 2nd century BC, which contained the values of sine for various angles. In the 6th century AD, Indian mathematician Aryabhata developed a formula for calculating sine using half-angle identities.
Inverse Sine
The inverse sine function, also known as the arcsine, is the function that undoes the sine function. It returns the angle whose sine is a given value.
| Function | Range | Inverse Function |
|---|---|---|
| Sine | [-1, 1] | Arcsine |
| Cosine | [-1, 1] | Arccosine |
| Tangent | (-∞, ∞) | Arctangent |
Last Recap
In conclusion, sine meaning encompasses a multifaceted concept that intertwines mathematical precision, graphical elegance, and practical utility. Its versatility extends across diverse fields, empowering engineers, musicians, scientists, and countless others to unravel the complexities of our world.
Question Bank: Sine Meaning
What is the mathematical definition of sine?
Sine is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right-angled triangle.
How is sine used in real-world applications?
Sine finds applications in various fields, including engineering, music, and physics. For instance, it is used to calculate the trajectory of projectiles, design musical instruments, and analyze sound waves.
What is the inverse sine function?
The inverse sine function, also known as arcsine, is the function that gives the angle whose sine is a given value.